report writing

I’ve settled for a “sketchy” understanding of the vast amount of literature that relates to my project. This has let me try to remember the take-home messages of a hundred papers or so, piece them together and attain a certain level of “proper” conversation with my supervisor. But it’s not helping with the literature review part of my report, which demands quite a lot more precision.

dang.

some physics, why not

Mostly for my benefit, I’m looking for a simple way to compare the canonical and grand canonical ensembles in statistical physics. How about this…

– – –

The canonical ensemble is a load of “systems”, each of which has a set of energy levels, and can exchange energy with all the other systems.

The probability of a system being in the ith state, whose energy is E_i, is:

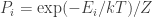
where Z is the system’s partition function.

The systems don’t have to be identical, but different systems have different Z’s.

– – –

The grand canonical ensemble is a load of “systems”, each of which has a set of “legal” particle numbers: 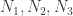, … (probably 0, 1, 2…) and has a set of energy levels for each particle number, and can exchange energy and particles with all the other systems.

The probability of a system being in state (r,s), meaning it has particles and total energy 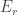, is:

where X is the system’s grand partition function. is called chemical potential. Now to explain that…